강 연결 성분(Strongly Connected Component)이란?
강 연결 성분이란 방향 그래프에서 연결 성분 내의 임의의 두 정점 u와 v에 대해서 u에서 v로 가는 경로가 있는 동시에, v에서 u로 돌아오는 경로가 있는 연결 성분이다.
강 연결 성분은 그 정의의 특징 상 단절 정점이나, 다리 간선을 포함하지 않는데, 생각해보면 당연하다. 강 연결 성분 내의 특정 정점을 제거함으로써, 두 개 이상의 연결 성분으로 나뉘지도 않고 그러한 간선도 존재하지 않는다.
아래 그림을 살펴보면, 그 의미를 더욱 쉽게 파악할 수 있을 것이다.
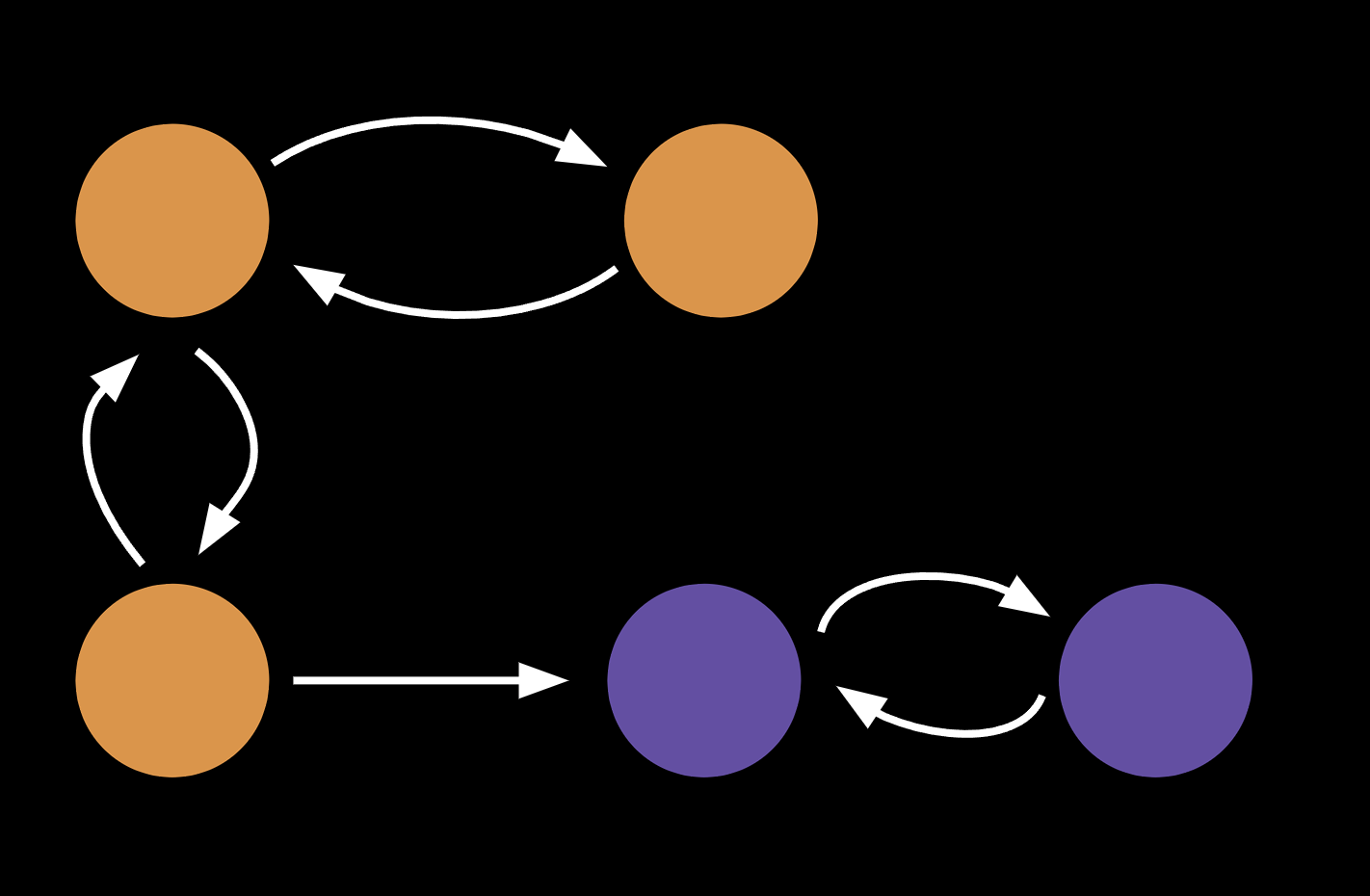
색이 같은 정점들을 한번 살펴보면, 임의의 두 정점에 대해서 오고 가는 길이 있다는 것을 확인할 수 있다. 반대로, 색이 다른 정점끼리 오고 가려면, 어느 한 방향은 막히고 만다.
궁극적으로, SCC의 목표는 이렇게 색이 같은 정점들의 집합을 찾아내는 것이다. 다시말해 그래프에서 강 연결 성분을 찾아내는 것이라고 할 수 있다.
SCC 알고리즘의 종류로는 두 가지로, Tarjan 알고리즘, Kosarasu 알고리즘이 있다.
Kosarasu 알고리즘은 역방향 그래프 사용하며 2번의 DFS를 거치고,Tarjan 알고리즘은 스택을 사용하며, 1번의 DFS를 거친다.
이번 포스팅에서는 Kosarasu 알고리즘과 Tarjan 알고리즘을 통해 손쉽게 강 연결 성분을 찾아볼 것이다.
Kosarasu 알고리즘 이해하기
Kosarasu 알고리즘은 강 연결 성분(SCC)의 개념과 위상 정렬에 대해 알고 있다면, 쉽게 터득할 수 있는 알고리즘이다.
위상 정렬에 대하여 잘 모른다면, 아래 포스팅을 통해 개념을 습득한 뒤 보는 것을 추천한다.
[알고리즘] 위상 정렬을 이해해보자.
* 이 글은 알고리즘에 관해 학습하며 정리한 글입니다. 틀린 점이나, 고쳐야 할 부분이 있으면 알려주세요..! 위상 정렬이란? 위상 정렬이란(Topological Sort) : 사이클이 없는 방향 그래프(Directed Acycl
devrepo.tistory.com
위상 정렬이라 함은 사이클이 없는 방향 그래프에서 정점을 선형 순서로 나타낸 것이라고 하였다. 이는 정점들 간의 우선 순위를 나타내기 위해 사용된다. 또한 앞선 내용에서 강 연결 성분은 두 정점 간에 오고 가는 방향이 존재하다는 것을 우리는 알고 있다.
Kosarasu의 핵심 개념은 바로 이 위상 정렬을 통해서 정점을 선형 순서로 나타내고, 기존의 그래프의 방향을 반대로 뒤집은 역방향 그래프를 사용하는 것이다. 이후, 위상 정렬의 정점 순서대로 강 연결 성분을 찾기 시작하는데 이때 역방향 그래프에서 해당 방향으로 이동할 때 갈 수 있는 정점들을 출력하면 된다.
갈 수 있는 정점들은 곧, 위상 정렬에서 찾은 선형 순서로도 방문이 가능하며 그 역순의 방향으로도 가능하다는 의미이기도 하다. 즉, 갈 수 있는 정점들이란 강 연결 성분을 말한다.
헷갈리면 안되는 것이 위상 정렬의 순서대로 정점을 고르고, 그 정점이 위치한 역방향 그래프에서 실질적으로 강 연결 성분이 되는 정점들을 찾는 것이다. 이때 DFS를 사용해 정점을 찾을 수 있다.
굳이 위상 정렬의 순서대로 골라야 하느냐? 라는 의문점도 생길 수 있다. 하지만 위상 정렬의 순서대로 고르지 않는다면, 각 SCC 내부에서 위상 정렬 순서를 지키지 못할 수 있다. 결국 위상 정렬 순서를 지키며 오고 가는 방향이 존재함을 나타내야 하기 때문이다.
다시말해, 위상 정렬의 순서는 우선 순위가 정해진 정점들의 순서이다. 그 순서 자체는 지키며 가야한다는 것을 염두해 두자.

위와 같은 그래프가 있다고 하자. 이 그래프에서 위상 정렬은 S = [8 9 2 3 5 6 0 1 7 4] 이다. 이 위상 정렬 요소의 순서대로 역방향 그래프안에 있는 SCC를 찾으면 된다. 아래 그림은 한번 보자.

위 그래프는 기존의 방향 그래프를 역으로 뒤집은 방향 그래프이다. 해당 방향 그래프에서 결국 SCC를 찾을 건데, 그 순서는 위상 정렬의 순서에 기반한다.
S에서 8이 위상 정렬 내에 가장 앞순이므로, 8부터 탐색하면, 8-2-9 그 다음은 나오지 않는다.
그러면 S에서 남은 요소는 S = [3 5 6 0 1 7 4] 이다. 이후, 3부터 탐색하면, 3-0-6 이 나오며, S = [5 1 7 4]가 된다.
5를 탐색하면, 5만이 나오며 S = [1 7 4]이고 나머지 값들은 그대로 SCC가 된다.
지금까지 동작 과정을 파악했으니, 한 번 코드로 봐보자.
Kosarasu 알고리즘 구현하기
import java.util.*;
public class KosarajuSCC {
private int V;
private List<Integer>[] graph;
private List<List<Integer>> sccList;
public KosarajuSCC(int V) {
this.V = V;
this.graph = new ArrayList[V];
for (int i = 0; i < V; i++) {
graph[i] = new ArrayList<>();
}
this.sccList = new ArrayList<>();
}
public void addEdge(int u, int v) {
graph[u].add(v);
}
public List<List<Integer>> findSCCs() {
Stack<Integer> stack = new Stack<>();
boolean[] visited = new boolean[V];
// 위상 정렬 만들기, 이때 DFS 수행이 동반됨.
for (int i = 0; i < V; i++) {
if (!visited[i]) {
fillOrder(i, stack, visited);
}
}
// 역방향 그래프
List<Integer>[] reversedGraph = new ArrayList[V];
for (int i = 0; i < V; i++) {
reversedGraph[i] = new ArrayList<>();
}
for (int i = 0; i < V; i++) {
for (int v : graph[i]) {
reversedGraph[v].add(i);
}
}
Arrays.fill(visited, false);
// stack은 위상 정렬, 앞에서 부터 하나씩 빼가면서 DFS 수행
while (!stack.isEmpty()) {
int v = stack.pop();
if (!visited[v]) {
// scc에 만들어진 강 연결성분 추가
List<Integer> scc = new ArrayList<>();
DFSUtil(reversedGraph, v, visited, scc);
sccList.add(scc);
}
}
return sccList;
}
// 위상 정렬 만들기 위한 DFS
private void fillOrder(int u, Stack<Integer> stack, boolean[] visited) {
visited[u] = true;
for (int v : graph[u]) {
if (!visited[v]) {
fillOrder(v, stack, visited);
}
}
stack.push(u);
}
// scc를 찾기 위한 DFS
private void DFSUtil(List<Integer>[] reversedGraph, int v, boolean[] visited, List<Integer> scc) {
visited[v] = true;
scc.add(v);
for (int i : reversedGraph[v]) {
if (!visited[i]) {
DFSUtil(reversedGraph, i, visited, scc);
}
}
}
public static void main(String[] args) {
KosarajuSCC g = new KosarajuSCC(5);
g.addEdge(1, 0);
g.addEdge(0, 2);
g.addEdge(2, 1);
g.addEdge(0, 3);
g.addEdge(3, 4);
List<List<Integer>> sccs = g.findSCCs();
for (List<Integer> scc : sccs) {
System.out.println(scc);
}
}
}
앞서 설명한 내용과 주석이 달린 내용을 보면, 쉽게 내용을 이해할 수 있을 것이다.
Tarjan 알고리즘 이해하기
Tarjan 알고리즘은 처음 배울 때는 앞선 Kosarasu 알고리즘보다 어렵다고 하는데, 개인적으로 이중 연결 요소에 대해 숙지했다면 더 쉽다고 생각한다. 또한 Tarjan 알고리즘이 kosarasu 알고리즘 보다 적용도 쉽다고 한다.
Tarjan 알고리즘은 앞선 Kosarasu 알고리즘과 달리 DFS를 한번만 호출한다. 이는 stack과 low 값을 이용하는 Tarjan 알고리즘의 특징이기도 하다.
이 알고리즘의 핵심은 low라는 값을 사용하는데, 이는 DFS 할 때 자기 자신을 포함해 도달할 수 있는 노드 ID가 가장 작은 값이다.
앞선 포스팅에서 배운 이중 연결 요소를 생각해보자. 이는 DFS 방문 순서를 담은 배열 dfsnum는 초기에는 동일한 값으로 지정된다. 같은 이중 연결 요소끼리는 이 dfsnum 중 가장 작은 값인 lownum으로 업데이트 한 것을 기억할 수 있다. 이는 재귀적으로 발생되고, 처음 방문한 정점에서 발생한다. 또한 사이클이 형성됨으로 인해 생성된 단절 정점을 통해 각자 다른 이중 연결 요소는 다른 lownum으로 지정해주었다.
[알고리즘] Biconnect Component : 이중 연결 성분
이중 연결 성분(Biconnect Component)란? 이준 연결 성분이란, 무방향 그래프의 연결 성분에서 임의의 두 점 사이에 적어도 두 개의 단순 경로가 존재하는 연결 성분을 뜻한다. 이때, 연결 성분이란 그
devrepo.tistory.com
마찬가지로 Tarjan도 유사하다.
dfn는 방문순서이며, low 값도 dfn 중 가장 작은 값을 의미한다. 초기에 정점 방문 시에는 dfn과 low값을 동일한 값으로 지정한다. 또한 처음 방문한 정점에서 같은 low 값으로 지정된다.
차이점이 있다면, 사이클을 형성하는 것 대신에 Stack 안에 방문한 정점들을 넣어 놓는다. 그리고 탐색 도중 Stack의 요소를 만난다면 더 이상 탐색은 중지하며 low를 업데이트 할 뿐이다. (사실 상 사이클을 형성하는 것과 같다고 본다.)
이후, SCC를 출력하기 위해 low[u]와 dfn[u]의 값이 일치하는 것을 확인한다. 이는 SCC의 값 중, 처음 스택에 넣은 값에서 SCC를 뽑아내기 위함이다.
그렇게 뽑아낸 SCC를 SCCS라는 강 연결 성분들을 모으는 리스트에 추가하며 진행하는 것이다.
다음으로 예제 코드를 보며 그 동작을 실질적으로 이해해보자.
Tarjan 알고리즘 구현하기
import java.util.*;
class TarjanAlgorithm {
private int sequence = 0;
private Stack<Integer> stack = new Stack<>();
private List<List<Integer>> graph;
private int[] dfn;
private int[] low;
private boolean[] inStack;
public List<List<Integer>> findStronglyConnectedComponents(List<List<Integer>> adjacencyList) {
int n = adjacencyList.size();
graph = adjacencyList;
dfn = new int[n];
low = new int[n];
inStack = new boolean[n];
Arrays.fill(dfn, -1);
Arrays.fill(low, -1);
List<List<Integer>> sccs = new ArrayList<>();
for (int u = 0; u < n; u++) {
if (dfn[u] == -1) {
stronglyConnected(u, sccs);
}
}
return sccs;
}
private void stronglyConnected(int u, List<List<Integer>> sccs) {
dfn[u] = low[u] = sequence++;
stack.push(u);
inStack[u] = true;
for (int w : graph.get(u)) {
if (dfn[w] == -1) {
stronglyConnected(w, sccs);
low[u] = Math.min(low[u], low[w]);
} else if (inStack[w]) {
low[u] = Math.min(low[u], dfn[w]);
}
}
if (low[u] == dfn[u]) {
List<Integer> scc = new ArrayList<>();
while (true) {
int x = stack.pop();
inStack[x] = false;
scc.add(x);
if (x == u) break;
}
sccs.add(scc);
}
}
public static void main(String[] args) {
List<List<Integer>> adjacencyList = new ArrayList<>();
int n = 6; // 그래프의 정점 수
for (int i = 0; i < n; i++) {
adjacencyList.add(new ArrayList<>());
}
adjacencyList.get(0).add(1);
adjacencyList.get(1).add(2);
adjacencyList.get(2).add(0);
adjacencyList.get(2).add(3);
adjacencyList.get(3).add(4);
adjacencyList.get(4).add(5);
adjacencyList.get(5).add(3);
TarjanAlgorithm tarjan = new TarjanAlgorithm();
List<List<Integer>> sccs = tarjan.findStronglyConnectedComponents(adjacencyList);
for (List<Integer> scc : sccs) {
System.out.println("Strongly Connected Component:");
for (int vertex : scc) {
System.out.print(vertex + " ");
}
System.out.println();
}
}
}
'🍀 Knowledge > 알고리즘' 카테고리의 다른 글
| [알고리즘] 최단 경로 알고리즘 - Dijkstra, Bellman-Ford, Floyd-Warshall 알고리즘 (1) | 2023.10.15 |
|---|---|
| [알고리즘] 최소 신장 트리(MST) - Kruskal, Prim, Sollin 알고리즘 (1) | 2023.10.14 |
| [알고리즘] Biconnect Component : 이중 연결 성분 (0) | 2023.10.12 |
| [알고리즘] 위상 정렬을 이해해보자. (1) | 2023.10.12 |
| [알고리즘] 유니온과 파인드 알고리즘(union, find) (0) | 2023.09.07 |
